机器学习平凡之路九

发表于 | 分类于 | 热度: ℃ |
字数统计: 2.3k | 阅读时长 ≈ 10

机器学习平凡之路九

  1. 集成学习
  2. 随机森林,梯度替身决策树,XGBoost算法
  3. 偏差和方差

集成学习

集成学习就是机器学习里面的协同作战。也相当于几个不大一样的模型组合起来，很可能效率会好过一个单独的模型

偏差和方差

偏差和方差是机器学习性能优化的风向标

方差定义是一组数据距离其均值的离散程度。机器学习的偏差用于衡量模型的准确程度

偏差的评判是机器学习模型的准确度。偏差越小，模型越准确。度量了算法预测与真实结果的离散程度。刻画了学习算法本身的拟合能力。好比每次打靶，比较靠近靶心

方差评判的是机器学习模型的稳定性，方差越小，模型越稳定。度量了训练集变动所导致的学习性能变化，刻画了数据扰动所造成的影响。每次打靶，不管打的准不准，击中点比较集中。

噪声,噪声表达的是在当前任务上任何学习算法所能达到的泛化误差的下界。刻画了学习问题本身的难度。属于不可约减的误差

降低偏差与方差

  1. 给定一个学习任务。模型对训练集的拟合不够完善，会出现高偏差
  2. 当充分训练后，训练好的模型应用于测试机，并不一定有好的效果。模型应用于不用的数据集，会出现高方差。也就是过拟合的状态
  3. 机器学习性能优化领域的最核心问题。就是寻找偏差和方差之间的最佳平衡点。训练集优化和测试集泛化的平衡点
  4. 性能优化是有顺序的，一般是先降低偏差，在聚焦于降低方差。
  5. 同样的数据集大小对偏差和方差的有一定的影响

Bagging算法-多个基模型的聚合

算法的基本思路是从原始数据集中抽取数据,形成K个随机的新训练集。然后训练处K个不同的模型。

过程如下:

  1. 每轮抽取n个训练样本(有些样本可能被多次抽取，有些样本可能一次都没有被抽取。叫做有放回的抽取，这个过程也叫做自助采样)
  2. 每次使用一个训练集得到一个模型，K个训练集得到K个模型。模型称作为基模型，基模型有两种情况:
    1. 分类问题，K个模型采用投票的方式得到分类结果
    2. 回归问题，计算K个模型的均值作为最后的结果.

树具有显著的低偏差，高方差的特点。Bagging算法,就从树模型开始，解决太过于精准，不易泛化的问题。

在Bagging中，有两种模型BaggingClassifier和BaggingRegressor用于分类问题和回归问题

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
import pandas as pd
df_bank = pd.read_csv('BankCustomer.csv')
# 二元类别进行数字化
df_bank['Gender'].replace('Female',0,inplace = True)
df_bank['Gender'].replace('Male',1,inplace = True)
# 显示数字类别
print(df_bank['Gender'].unique())
# 把多元类别转化为哑变量特征
d_city = pd.get_dummies(df_bank['City'], prefix = 'City')
df_bank = [df_bank,d_city]
df_bank = pd.concat(df_bank, axis=1)
# 构建特征和标签集合
y = df_bank['Exited']
X = df_bank.drop(['Name','Exited','City'] , axis = 1)
X.head()

image-20210406092823645

1
2
3
# 拆分数据集为测试集和训练集
from sklearn.model_selection import train_test_split 
X_train, X_test , y_train,y_test = train_test_split(X,y,test_size=0.2, random_state=0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 对多棵决策树进行聚合
from sklearn.ensemble import BaggingClassifier # 导入Bagging分类器
from sklearn.tree import DecisionTreeClassifier # 导入决策树分类器
from sklearn.metrics import (f1_score, confusion_matrix)
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
y_pred = dt.predict(X_test)
print(dt.score(X_test,y_test)*100)
print(f1_score(y_test,y_pred)*100)
bdt = BaggingClassifier(DecisionTreeClassifier())  # 默认的基模型数量为10
bdt.fit(X_train,y_train)
y_pred = bdt.predict(X_test)
print(bdt.score(X_test,y_test)*100)
print(f1_score(y_test,y_pred)*100)

image-20210406093742481

使用网格优化参数

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.model_selection import GridSearchCV
bdt_param_grid = {
    'base_estimator__max_depth' : [5,10,20,50,100],
    'n_estimators' : [1, 5, 10, 50]}
bdt_gs = GridSearchCV(BaggingClassifier(DecisionTreeClassifier()),
                   param_grid = bdt_param_grid, scoring = 'f1',
                   n_jobs= 10, verbose = 1)
bdt_gs.fit(X_train, y_train)
bdt_gs = bdt_gs.best_estimator_ # 最佳模型
y_pred = bdt.predict(X_test)
print(bdt_gs.score(X_test,y_test)*100)
print(f1_score(y_test,y_pred)*100)

image-20210406095807759

从树的聚合到随机森林

假设树分叉时选择的特征数m

  1. 对于分类问题，m可以设置为特征数的平方根
  2. 对于回归问题，m可以设置为特征数的1/3

RandomForestClassifier 和 RandomForestRegressor分别适用于分类问题和回归问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier()
rf_param_grid = {
    'max_depth' : [None],
    'max_features' : [1,3,10],
    'min_samples_split':[2,3,10],
    'min_samples_leaf':[1,3,10],
    'bootstrap':[True,False],
    'criterion':['gini']
}
rf_gs = GridSearchCV(rf,param_grid = rf_param_grid,
                    scoring= 'f1',n_jobs =10,verbose=1
                    )
rf_gs.fit(X_train,y_train)
rf_gs = rf_gs.best_estimator_
y_pred = rf_gs.predict(X_test)
print(rf_gs.score(X_test,y_test)*100)
print(f1_score(y_test,y_pred)*100)

image-20210406100939946

使用极端森林

极端森林不去考领所有的分支，而是随机选择一些分支，从中拿到一个最优解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.ensemble import ExtraTreesClassifier
ext_param_grid = {"max_depth": [None],
              "max_features": [1, 3, 10],
              "min_samples_split": [2, 3, 10],
              "min_samples_leaf": [1, 3, 10],
              "bootstrap": [True,False],
              "n_estimators" :[100,300],
              "criterion": ["gini"]}
ext_gs = GridSearchCV(ext,param_grid = ext_param_grid, scoring="f1", 
                     n_jobs= 4, verbose = 1)
ext_gs.fit(X_train,y_train) # 拟合模型
ext_gs = ext_gs.best_estimator_ # 最佳模型
y_pred = ext_gs.predict(X_test) # 进行预测
print(rf_gs.score(X_test,y_test)*100)
print(f1_score(y_test,y_pred)*100)

image-20210406102805547

需要注意的点:

  1. 随机森林在大多数情况下优于极端森林
  2. 极端森林不考虑所有的分支，速度比较快
  3. 某些数据，极端森林拥有更强化的泛化能力。

Boosting算法

  1. 每一轮的中有针对性的改变训练数据
  2. 集成弱模型，不断的进行选择优化

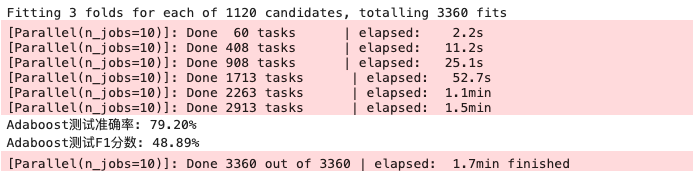
AdaBoost算法

给不同的样本分配不同的权重,分错的样本权重在过程中增大。新模型会更加关注这些被分错的样本，然后将修改过权重的新数据集输入下层模型进行训练。最后将每次得到基模型组合起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.ensemble import AdaBoostClassifier # 导入AdaBoost模型
dt = DecisionTreeClassifier() # 选择决策树分类器作为AdaBoost的基准算法
ada = AdaBoostClassifier(dt) # AdaBoost模型
# 使用网格搜索优化参数
ada_param_grid = {"base_estimator__criterion" : ["gini", "entropy"],
                  "base_estimator__splitter" :   ["best", "random"],
                  "base_estimator__random_state" :   [7,9,10,12,15],
                  "algorithm" : ["SAMME","SAMME.R"],
                  "n_estimators" :[1,2,5,10],
                  "learning_rate":  [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3,1.5]}
ada_gs = GridSearchCV(ada,param_grid = ada_param_grid, 
                        scoring="f1", n_jobs= 10, verbose = 1)
ada_gs.fit(X_train,y_train) # 拟合模型
ada_gs = ada_gs.best_estimator_ # 最佳模型
y_pred = ada_gs.predict(X_test) # 进行预测
print("Adaboost测试准确率: {:.2f}%".format(ada_gs.score(X_test, y_test)*100))
print("Adaboost测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

image-20210406104759255

梯度提升

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.ensemble import GradientBoostingClassifier # 导入梯度提升分类器
gb = GradientBoostingClassifier() # 梯度提升分类器
# 使用网格搜索优化参数
gb_param_grid = {'loss' : ["deviance"],
                 'n_estimators' : [100,200,300],
                 'learning_rate': [0.1, 0.05, 0.01],
                 'max_depth': [4, 8],
                 'min_samples_leaf': [100,150],
                 'max_features': [0.3, 0.1]}
gb_gs = GridSearchCV(gb,param_grid = gb_param_grid,
                     scoring="f1", n_jobs= 10, verbose = 1)
gb_gs.fit(X_train,y_train) # 拟合模型
gb_gs = gb_gs.best_estimator_ # 最佳模型
y_pred = gb_gs.predict(X_test) # 进行预测
print("梯度提升测试准确率: {:.2f}%".format(gb_gs.score(X_test, y_test)*100))
print("梯度提升测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

image-20210406105111526

XGBoost算法

一般叫做极端梯度提升

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from xgboost import XGBClassifier # 导入XGB分类器
xgb = XGBClassifier() # XGB分类器
# 使用网格搜索优化参数
xgb_param_grid = {'min_child_weight': [1, 5, 10],
                  'gamma': [0.5, 1, 1.5, 2, 5],
                  'subsample': [0.6, 0.8, 1.0],
                  'colsample_bytree': [0.6, 0.8, 1.0],
                  'max_depth': [3, 4, 5]}
xgb_gs = GridSearchCV(xgb,param_grid = xgb_param_grid,  
                     scoring="f1", n_jobs= 10, verbose = 1)
xgb_gs.fit(X_train,y_train) # 拟合模型
xgb_gs = xgb_gs.best_estimator_ # 最佳模型
y_pred = xgb_gs.predict(X_test) # 进行预测
print("XGB测试准确率: {:.2f}%".format(xgb_gs.score(X_test, y_test)*100))
print("XGB测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

image-20210406105931771

对于很多浅层回归和分类。Boosting算法都是生成一棵树后根据反馈，生成另一颗树

Bagging是降低方差,利用基模型的独立性.Boosting是降低偏差,基于同一个模型

Voting算法

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.ensemble import  VotingClassifier # 导入Voting分类器
# 把各种模型的分类结果进行Voting，同学们还可以加入更多模型如SVM，kNN等
voting = VotingClassifier(estimators=[('rf', rf_gs),
                                      ('gb',gb_gs),
                                      ('ext', ext_gs),
                                      ('xgb', xgb_gs),
                                      ('ada', ada_gs)],

                          voting='soft', n_jobs=10)
voting = voting.fit(X_train, y_train) # 拟合模型
y_pred = voting.predict(X_test) # 进行预测
print("Voting测试准确率: {:.2f}%".format(voting.score(X_test, y_test)*100)) 
print("Voting测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))

image-20210406110007127

Stacking算法

步骤1 定义stacking方法

1
2
3
4
5
6
7
8
9
10
11
12
13
# stacking
from sklearn.model_selection import StratifiedKFold # 导入K折验证工具
def Stacking(model,train,y,test,n_fold): # 定义Stacking函数
    folds = StratifiedKFold(n_splits=n_fold,random_state=1)
    train_pred = np.empty((0,1),float)
    test_pred = np.empty((0,1),float)
    for train_indices,val_indices in folds.split(train,y.values):
        X_train,x_val = train.iloc[train_indices],train.iloc[val_indices]
        y_train,y_val = y.iloc[train_indices],y.iloc[val_indices]
        model.fit(X=X_train,y=y_train)
        train_pred = np.append(train_pred,model.predict(x_val))
    test_pred = np.append(test_pred,model.predict(test))
    return test_pred,train_pred

步骤2 导入基模型

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.tree import DecisionTreeClassifier # 导入决策树模型
model1 = DecisionTreeClassifier(random_state=1) # model1-决策树
test_pred1 ,train_pred1 = Stacking(model=model1,n_fold=10,
                train=X_train,test=X_test,y=y_train)
train_pred1 = pd.DataFrame(train_pred1)
test_pred1 = pd.DataFrame(test_pred1)
from sklearn.neighbors import KNeighborsClassifier # 导入kNN模型
model2 = KNeighborsClassifier() # model2-kNN
test_pred2 ,train_pred2 = Stacking(model=model2,n_fold=10,
                                 train=X_train,test=X_test,y=y_train)
train_pred2 = pd.DataFrame(train_pred2)
test_pred2 = pd.DataFrame(test_pred2)

步骤3 使用全新的数据集，以及不必与基模型有关联

1
2
3
4
5
6
7
# Stacking的实现-用逻辑回归模型预测新特征集
X_train_new = pd.concat([train_pred1, train_pred2], axis=1)
X_test_new = pd.concat([test_pred1, test_pred2], axis=1)
from sklearn.linear_model import LogisticRegression # 导入逻辑回归模型
model = LogisticRegression(random_state=1)
model.fit(X_train_new,y_train) # 拟合模型
model.score(X_test_new, y_test) # 分数评估

image-20210406112048088