机器学习之平凡之路八
- 经典算法
- 如何寻找最佳算法,优化参数
经典算法
- KNN-邻居是哪一类我就是哪一类
- SVM-以前比神经网络还火
- 朴素贝叶斯-简单概率分类算法
- 决策树-无数个if与else的集合
- 随机森林-很多棵决策树的集成
K最近邻
K最近邻意思是K个最近的邻居,对于需要贴标签的数据样本,总会找几个和自己离得最近的样本。也就是邻居,看看邻居的标签是什么。如果邻居中大多数样本都是某一类样本。它就认为自己也是这一类样本。参数K通常是不超过20的数据
向量的距离:欧式距离和曼哈顿距离
欧式距离是欧几里得空间中两点间的普通距离
曼哈顿距离是方格线距离或城市区块距离,是两个点在标准坐标系上的绝对轴距的总和
两种向量距离就是L1范数(曼哈顿)和L2范数(欧氏)的定义
数据操作
1 | import numpy as np |
KNN
1 | from sklearn.neighbors import KNeighborsClassifier |

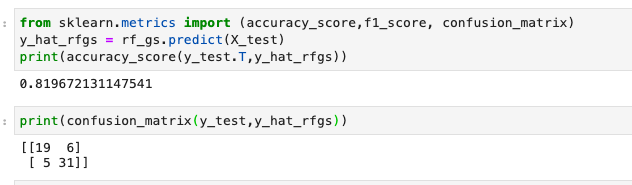
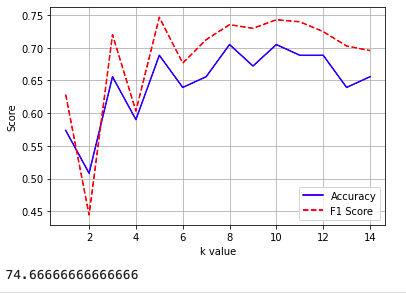
如何判定最佳K值
1 | # 寻找最佳K值 |
支持向量机
SVM支持向量机原理

超平面用于特征空间根据数据的类别切分出来的分界平面.支持向量,离当前超平面最近的数据点。在上图一个数据集的特征空间中,存在很多种可能的类分割超平面。SVM就是要在支持向量的帮助下找到最优的分类超平面.目标就是支持向量到超平面之间的垂直距离最宽。
对于线性可分
1 | from sklearn.svm import SVC |
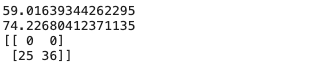
对于非线性分类
SVM通过核方法。
1 | svm.SVC(kernel='poly', degree=3) |
决策树
本质其实就是一个人想一个东西或者一个人。其他随便提问,本人只能回答是和不是.其实就是决策树,可以应用回归或者分类的问题
关于熵和特征节点的选择
熵度量信息的不确定性,信息的不确定性越大,熵就越大
- 信息熵代表随机变量的复杂度,也就是不确定性
- 条件熵代表某一个条件下,随机变量的复杂度
- 信息增益等于信息熵减去条件熵,代表了某个条件下。信息的复杂度减少的程度
如果一个特征从不确定到确定,过程对结果的影响比较大的话,可以认为这个特征分类能力比较强。熵减少得越多,信息增益就最大
决策树因为可以细分得很细,所以很容易出现过度拟合的状态。解决方式可以考虑为决策树进行剪枝。先剪枝:分支的过程中,熵减少量小于某一个阈值时,停止分支的创建。后剪枝:先创建完成的决策树,然后尝试消除多余的节点
1 | from sklearn.tree import DecisionTreeClassifier |

随机森林
n_estimators:要生成的树的数量
criterion:信息增益指标,可以选择gini或者entropy
bootstrap:可选择是否使用bootstrap方法取样,选择False,所有树基于原始数据集生成
max_features:通常由算法默认确定,对于分类问题,默认值是总特征数的平方根
1 | from sklearn.ensemble import RandomForestClassifier |

如何选择最佳机器学习算法

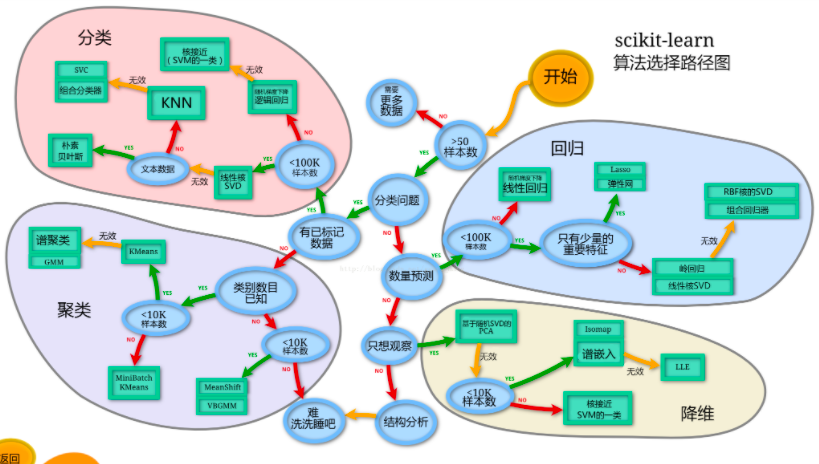
用网格搜索超参数调优
通过利用Sklearn的网格搜索。为特定的机器学习算法找到一个超参数的范围找到最佳值
1 | from sklearn.model_selection import StratifiedKFold # 导入k折验证工具 |