机器学习平凡之路五
- 神经网络的原理
- 神经网络的实现和实战
神经网络的原理
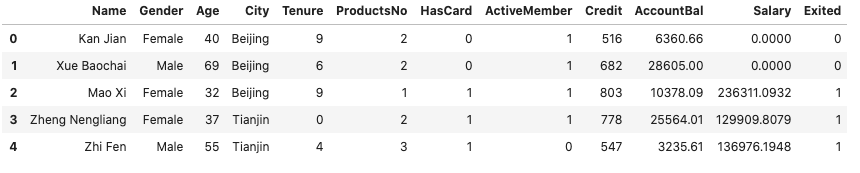
用过加载银行客户流失的数据,通过机器判断出哪些客户未来两年结束在该银行的业务,本质上也是分类。但是利用神经网络解决这类问题的优势
神经网络在计算机视觉,语音识别,自然语言处理,棋类竞赛和机器人技术
在数据集中,特征的维度组合越来越大,机器学习的过程中,单纯用线性回归和逻辑回归模型进行机器学习就力不从心。
特征空间是数据特征形成的空间,特征维度越高,特征空间越复杂,假设空间是假设函数形成的空间,特征越多,特征和标签之间的对应关系越难拟合。假设空间越复杂
深度学习的机理其实就是用一串一串的函数作用于输入数据,进行从原始数据到分类结果的过滤与提纯。这些层通过权重来参数化。通过损失函数来判断当前网络的效能,通过优化器太调整权重。寻找输入到输出的最佳函数。
注意:层就是神经网络的基本元素。神经网络是通过不同类型的层来构建的。
神经网络的实现和实战
数据分析与准备
1 | import numpy as np |
1 | import matplotlib.pyplot as plt |
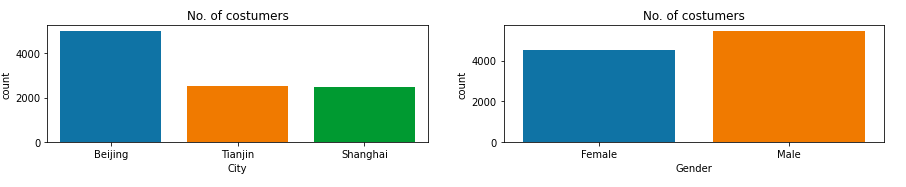
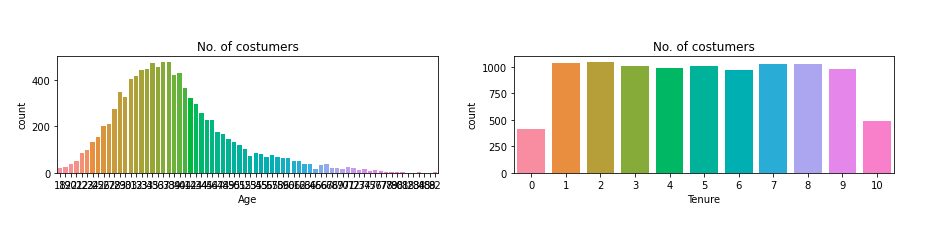
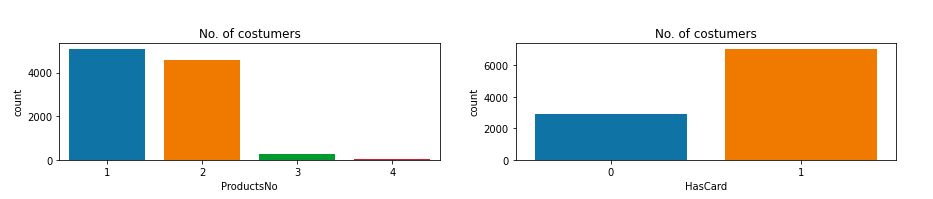
可以看出,北京的客户最多,男女客户的比例大致一致。年龄和客户数据量呈现正态分布
关于数据的处理准备工作
- 性别:这是一个二元类的特征。需要做0和1的转换
- 城市:这是一个多元类的特征,可以转换为多个二元类别的哑变量
- 姓名可以进行忽略处理
1 | # 二元类别进行数字化 |

1 | # 拆分数据集为测试集和训练集 |
使用逻辑回归算法尝试
1 | from sklearn.linear_model import LogisticRegression |
通过逻辑回归,我们可以看到准确率大概在78.3,当然使用神经网路至少看能不能提升准确率
学习keras
keras构建出来的神经网络模型通过模块组装在一起。各个深度学习元件是Keras模块,比如神经网络,损失函数,优化器,参数初始化,激活函数,模型曾泽华,都是可以组合起来构建新模型的模块
1 | import tensorflow as tf |

这个网络只有3层,493个参数.
模型可视化
1 | from IPython.display import SVG # 实现神经网络结构的图形化显示 |
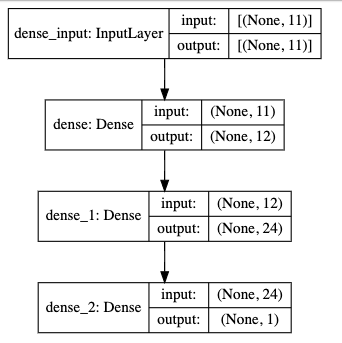
名词解释
- 模型的创建: 通过Sequential创建了一个序贯神经网络模型.与之对外的还有另外一种模型,称作为函数式API
- 输入层,通过add方法一层一层的进行顺序堆叠
- Dense是层的类型,代表密集网络层。也是全连接层
- input_dim是输入维度,输入维度必须与特征维度相同
- unit是输出维度,代表线性变化和激活之后的假设空间维度,也就是神经元的个数
- activation是激活函数,每一层都要设置的参数。relu书神经网络常用的激活函数
- 隐层不需要指定输入维度。
- 输出层,指定的输出维度是1.对于二分类问题,输出维度必须是1,如果是多分类问题。多少个类别,维度就是多少。对于二分类问题,Sigmoid是固定的选择。如果是神经网络输出层不用指定任何激活函数
1 | # 编译网络,指定优化器,损失函数,以及评估指标 |
- 优化器可以选择adam或者是rmsprop
- 损失函数二元分类使用二元交叉熵函数,神经网络使用均方误差函数是合适的选择
- 评估指标通过acc,也就是准确率
关于全连接层
一般用于处理最普通的机器学习向量数据,也就是2D张量数据集,公式为:
Output = Activation(dot(input,kernel)+bias)
神经网络的其它类型层
- 循环层,Kears的LSTM层,用于处理保存形状为(样本,时戳,标签)的3D张量中的序列数据
- 二维卷积层,Keras的Conv2D层。用于处理保存形状为(样本,帧数,图像高度,图像宽度,颜色深度)的4D张量中的图像数据
- 层就是相当于乐高的积木。将相互兼容,相同或者不同类型的多个层拼接在一起。
训练单隐层神经网络
需要注意的地方:样本中训练集的维度是12,所以前面的代码需要稍微调整下输入样本的维度为12
1 | history = ann.fit(X_train, y_train, |

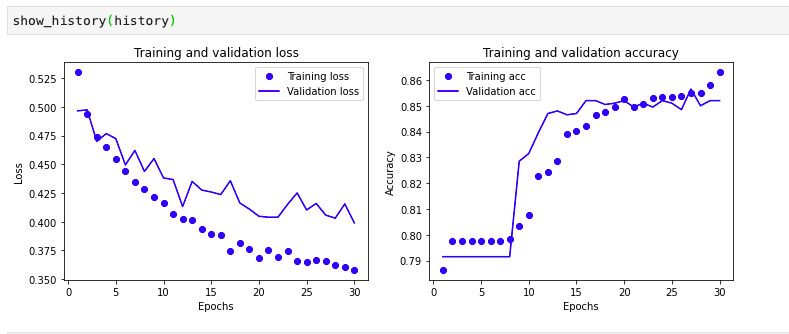
通过图示显示
1 | def show_history(history): # 显示训练过程的学习曲线 |
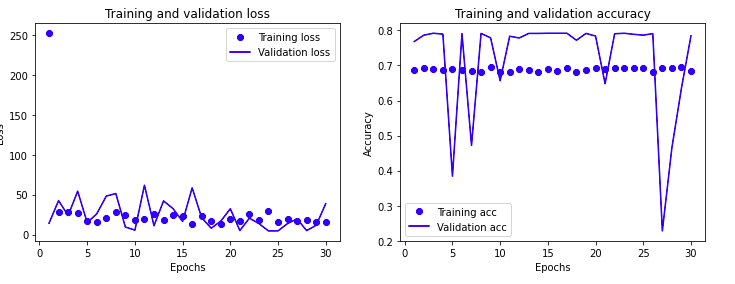
通过手段调优
混淆矩阵,精确率,召回率和F1分数
注意上面的问题:根据最上面的数据分析,按照80和20的比例,准确率80以下什么也没做。提升还是需要从每一个类别预测精确率和召回率上面入手
也就是说:对于这种大量标签是普通值,小部分标签是特殊值的数据集来说,3个标准的重要性要高于准确率
使用分类报告和混淆矩阵
1 | from sklearn.metrics import classification_report |
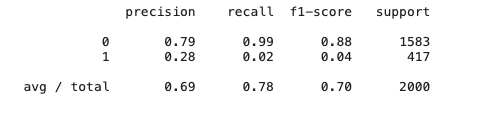
报告分别对应: 精确率,召回率,以及F1分数,对于客户标签为1的类别分数都为0,如果输出y_pred呈现清一色的0值
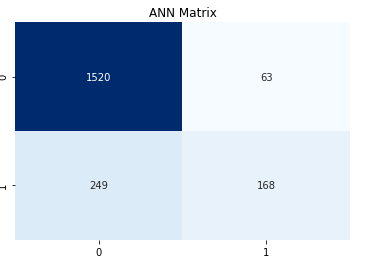
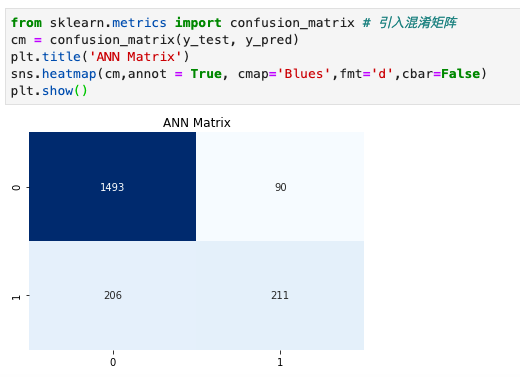
1 | from sklearn.metrics import confusion_matrix # 引入混淆矩阵 |
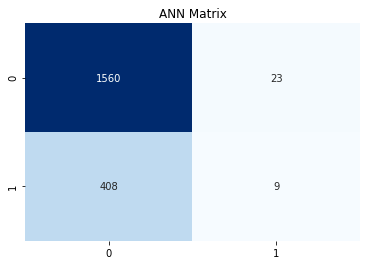
通过预测值和真值组成的矩阵,4个象限从上到下,从左到右,分别为真负,假正,假负,真正
也就是数据集真值,预测为负的有408个。这个和数据分析出来的值不对等,需要调整
解决问题
特征缩放的魔力
1 | # 通过特征缩放 |
分别使用逻辑回归和单层神经网络
1 | from sklearn.linear_model import LogisticRegression |
结果可以达到80%
1 | history = ann.fit(X_train, y_train, |

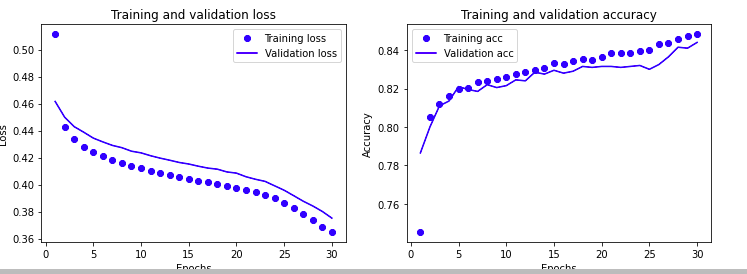
1 | from sklearn.metrics import classification_report |
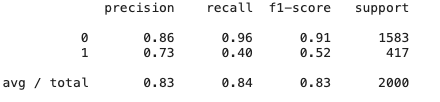
其他
在面对数据不平衡的时候,可以考虑阈值调整,欠采样,过采样
从单层到深度
深度神经网络就如宇宙一样,并不复杂,就是很多而已
优化
深度神经网络的梯度下降参数和参数优化过程是通过优化器实现的,包含了正向传播和反向传播
正向传播
- 从输入层开始,线性处理权重和偏置后。层层递进,然后计算出损失值的过程
反向传播
- 从结果开始,拿到损失函数给出的值,通过求导和偏微分逐步的发现每一个参数往哪个方向上面调整,减小损失
可调超参数
- 优化器
- 激活函数
- 损失函数
- 评估指标
关于梯度下降
神经网络权重参数随机初始化
1 | ann.add(layers.Dense(units=12, input_dim=12, |
批量梯度下降
1 | 配置batch_size |
随机梯度下降
1 | ann.compile(loss = keras.losses.categorical_crossentropy, |
小批量梯度下降
1 | keras.optimizers.SGD(lr=0.02, # 学习速率 |
动量SGD
更新参数W时不仅考虑当前梯度,还要考虑上一次的参数更新
1 | keras.optimizers.SGD(lr=0.02, # 学习速率 |
NAG上坡减少动量
1 | keras.optimizers.SGD(lr=0.02, # 学习速率 |
自适应梯度
1 | keras.optimizers.adagrad() |
加权平均值计算二阶动量
1 | keras.optimizers.RMSprop() |
Adam(常用)
1 | keras.optimizers.Adam( |
Nadam
1 | keras.optimizers.Adam( |
神经网络超参数的调试,没有一定之规矩,需要逐渐累积经验
激活函数
- Sigmoid函数映射在0和1之间
- Tanh函数映射在-1和1之间
- Relu函数算是主流,输入小于等于0时,输出是0,输入信号大于0是,输出等于输入
- Sigmoid用于二元分类,SoftMax用于多元分类
损失函数
- 对于连续值向量的回归问题
loss = 'mse' # 均方误差损失函数 - 对于二分类问题
loss = 'binary_crossentropy' # 二元交叉熵损失函数 - 对于多分类问题
loss = categorical_crossentropy # 分类交叉熵损失函数,如果输出是one-hot编码 - 对于多分类问题
loss = sparse_categorical_crossentropy # 稀疏分类交叉熵损失函数,如果输出是整数数值
评估指标
- 对于回归问题使用MAE和准确率比较常见
- 普通分类通过辅以精确率,召回率,F1分数等其他评估指标
重新定义(加入Dropout)
1 | ann = tf.keras.Sequential() # 创建一个序贯ANN模型 |


调试以及性能优化
通过回调功能,也就是根据一些预设的指示对训练进行控制
- ModelCheckpoint: 在训练过程中不同时间点保存模型,保存当前网络的所有权重
- EarlyStopping:如果验证损失不再改善,则中断训练
- ReduceLROnPlateau:训练过程中动态调节某些参数数值,跳出高原区,也就是局部地点或者鞍点
- TensorBoard:将模型训练过程可视化
1 | from tensorflow.keras.callbacks import ModelCheckpoint |
解决过度拟合与梯度消失和爆炸
过度拟合
- 能够用较小的网络解决问题,就不要强迫使用较大的网络
- 先使用少量数据训练一个较小的模型。小模型泛化好。
- 通过加入Dropout层。但是会对训练的速度有一定的影响
- 通过正则化解决过度拟合
梯度爆炸和梯度消失
本质原因就是网络太深,网络权重更新不稳定造成的。本质都是梯度反向传播中的连锁效应
选择合适的激活函数
1
2
3
4from keras import regularizers
model.add(Dense(64, input_dim=64,
kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=regularizers.l1(0.01))) # 使用过神经元权重进行正则化1
ann.add(BatchNormalization())
通过批标准化可以使网络中间层的输入数据分布变得更加均衡。加速网络的收敛,减少训练的次数