机器学习平凡之路二
- 数学知识
- python部分基础
数学
函数
函数视为一种模型,这种模型是对客观世界复杂事物之间的关系简单模拟
在函数中,一个事物输出随着另一个事物的输入的变化而变化
函数的输入和输出,很多情况下都是数字.函数也可以反映非数学之间的关系
函数需要注意的是输入集中的每一个元素X都要被照顾到。函数的输出值是独一无二的
机器学习中的函数
机器学习基本上等价于寻找函数的过程,机器学习到的函数,实现了从特征到结果的一个特定推断。机器学习不是注重特征到标签之间的因果逻辑,更多的是注重期间的相关关系
四方上下曰宇,往故来今曰宙。仰光宇宙之大,俯察品类之盛
如果决定是一个好函数,训练集和验证集上的预测准确并且能够泛化到测试集中,就是好函数
机器学习算法得到的函数,往往能看到数据背后隐藏着的,肉眼不能发现的秘密
机器学习算法,可以得到不同的函数。深度学习的函数相当于一大堆线性函数的跨层堆叠。不管什么样的学习,都是对样本集中特征到标签的关系总结。
函数分类
线性函数
线性函数只拥有一个变量一阶多项式函数,函数就和直线一样,比如y=-x+5或者y=0.5x+2,线性函数适合模拟简单的关系。比如房屋面积和期售价之间可能会呈线性关系
二次函数和多次函数
函数中自变量X中最大的指数被称为函数的次数。比如y=x的二次方,二次函数是凸函数,随着函数的次数升高,将不再是只有一个最低点的凸函数,此事将出现局部最低点
激活函数
激活函数在机器学习算法中实现的是非线性,阶跃性质的变换
比如y=1(x>0),y=0(x<0)
比如Sigmoid函数,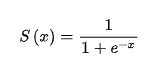 ,e是一个自然常数,约等于2.72
,e是一个自然常数,约等于2.72
比如ReLU函数,y=max(x,0)
比如Leaky ReLU函数,y=max(&x,x) . &代表斜率
对数函数
对数函数是指数函数的逆运算,原来的指数就是对数的底。
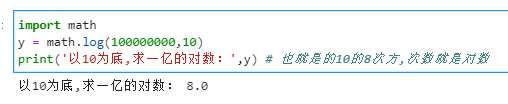
函数变化趋势
机器学习就是研究y如何随着X而变,通过求导和微分来实现的
导数是定义在连续函数的基础之上的,导数是引导,导航,它与函数上连续两个点之间变化趋势,也就是变化的方向相关
函数变化趋势至少由两个点体现,A趋近于B的时候,求其变换的极限。这就是导数。导数的值和它附近的一小段连续函数有关。如果没有那么一段连续的函数,就无法计算其切线的斜率。函数在该点也就是不可导的。
通过求导,实现了以直代曲。也发现了y值随X值变化的方向。也就是在机器学习中可以得到标签y随特征X而变化的方向。导数是针对一个变量而言的函数变化趋向,对于多元的函数,关于一个变量的导数为偏导数。
凸函数
凸函数可以沿着导数给出的方向滚到最低点。在机器学习中无法达到全局最低点是很不理想的情况
梯度
对多元函数的各参数求偏导数,然后把所求的各个参数的偏导数以向量的形式写出来,就是梯度
比如:下山,已知远处的位置比此处低很多。如何下山,每走一个位置求解当前的位置的梯度。然后沿着梯度的负方向,也就是往最陡峭的地方向下一步走。
梯度下降的作用:
- 机器学习的本质是找到最优的函数
- 如何衡量函数是否最优,方法是尽量减小预测值和真值间的误差
- 可以建立误差和模型参数之间的函数
- 梯度下降能够引导我们走到凸函数的全局最低端,也就是找到误差最小时的参数。
机器学习的数据结构
在机器学忠,用于存储数据的结构叫作张量。张量是机器学习程序中的数字容器。本质上就是各种不同维度的数组。
张量的维度称为轴axis。轴的个数称为阶(rank)。张量的形状(shple)就是张量的阶加上每个阶的维度
标量
scalar。包含一个数字的的张量,标量的功能主要用于流程控制,设置参数等。
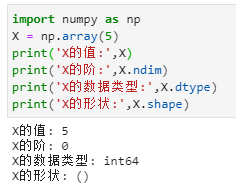
向量
有一组数字组成的数组叫做向量(vector),也就是一阶张量。

比如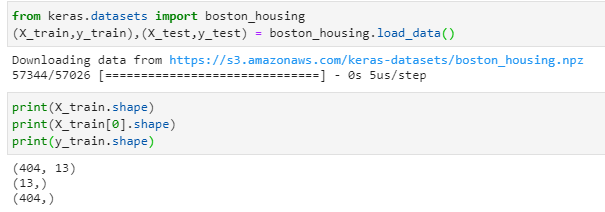
X_train是一个2D的矩阵,是404个样本数据的集合。y_train是一个向量,是一个404维的标签向量
向量的维度:表示沿着某个轴上的元素个数
而X_train[0],相当于是一个13维向量(也就是1D张量),简单的说就是包含13个特征
向量的点积
两个向量之间可以进行乘法运算,向量的点积结果是一个值,也就是一个标量,比如
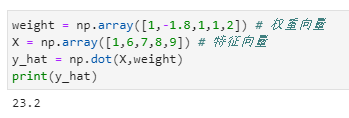
矩阵(2D张量)
矩阵是2D张量一般形状为 (样本轴,特征轴),比如城市交通数据集,包含城市的街道名,等28个交通数据特征。共800个街道。张量形状为(800,28)
矩阵的点积
矩阵相乘,第一个矩阵的列数必须等于第二个矩阵的行数。(m,n)乘以(n,m)得到一个矩阵(m,m),公式自行百度
序列数据

比如
第一轴: 样本轴,一年记录下来的数据共365个。也就是365维向量
第二轴:时间步轴,每天一共24小时,每小时4个15分钟,共96维
第三轴:特征轴,一共是温度,湿度,风力3个维度
也就是对于时间数据集的形状为3D张量(样本,时间,标签)
图像数据
图像数据本身包含高度,宽度,在加上颜色深度的通道。对于图像数据集来说形状为(样本,图像高度,图像宽度,颜色通道)
在机器学习中,数据是一批一批的进行处理
视频数据
视频数据需要5D张量也就是(样本,帧,高度,宽度,颜色深度)
python中张量的创建和运算
机器学习中张量大多是通过Numpy数组来实现的

创建数组
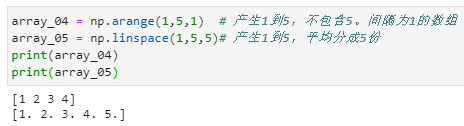
机器学习一般先从文本文件中把所有样本读取到Dataframe格式的数据,然后用array方法转为Numpy数组,也就是变为张量。然后进行后续的操作
通过索引和切片访问张量中的数据
索引既是访问张量某个具体的数据
切片就是访问一个范围内的数据
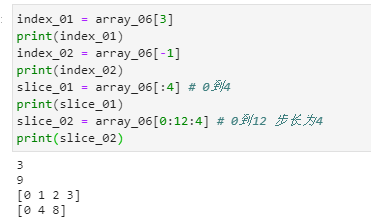
张量的操作
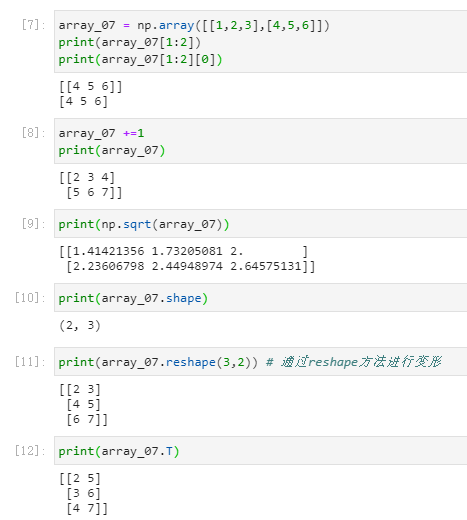
python中的广播
Python的广播功能就是自动自发地把一个变成一排的向量,把一个低维的数组变为高维的数组
张量的的形状和第一位加数保持一致
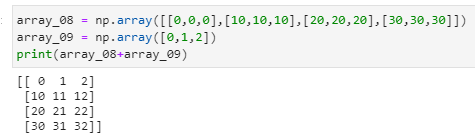
向量和矩阵的点积运算
向量a = [a1,a2,…,an]
向量b = [b1,b2,…,bn]
aXb = a1xb1+a2xb2 +…+anxbn
矩阵形状(a,b)和 (b,c)结果为(a,c)
概率
某公司男生和女生各占50%,烟民占总人数的10%,女烟民占1%,遇到一个烟民的概率可能性多大
事件B —-烟民
事件A —-女生
P(B) —-10% 随便遇到一个烟民的概率
P(A)—-50% 随便遇到一个女生的概率
p(B|A) 1% 已知100个人里面才有一个烟民 已知A ,B的概率
p(A|B) = 1% X 50% /10% = 5% 已知B,A的概率
条件概率就是已知事件发生的时候,前者的概率
这个就是贝叶斯定理
其他
正态分布 自行百度
标准差(sigma)是根据方差进行计算出来的。方差是一组资料中实际数值与算术平均数的差值做平方结果相加之后,除以总数,标准差是方差算术平方根
方差和标准差都是数据相对期望值的离散程度
一般数据标准化,就是样本特征值减去期均值,然后除以期标准差进行缩放